Calculadora de Z-score
A calculadora de Z-score é a ferramenta para quem precisa padronizar valores em uma distribuição normal, comparar dados de diferentes escalas ou determinar probabilidades associadas a eventos estatísticos.
Cálculo passo a passo da calculadora de Z-Score
Fórmula da operação:
O Z-Score mede quantos desvios padrão um valor está acima ou abaixo da média.
O que é escore padrão Z
O escore-z, também conhecido como escore padrão, é um dos conceitos mais importantes da estatística descritiva e inferencial. Pois, ele indica quantos desvios padrão um valor individual está distante da média de uma distribuição. Neste guia, você vai aprender não apenas o que é z-score, mas também como aplicar em diferentes contextos estatísticos.
Simplificando o conceito, o z-score transforma qualquer valor bruto em uma unidade padronizada que permite comparações justas entre conjuntos de dados distintos. Por exemplo, se um aluno tirou 85 em uma prova cuja média foi 75 e o desvio padrão foi 5, seu Z-score será \( Z = \frac{85 – 75}{5} = 2 \). Portanto, isso significa que sua nota está 2 desvios padrão acima da média. Entendeu a lógica? O z-score ajuda você a avaliar desempenhos relativos, identificar outliers, calcular probabilidades e construir modelos preditivos.
Além disso, aprender a calcular z-scores desenvolve habilidades analíticas que facilitam a compreensão de métodos estatísticos avançados, como regressão linear, análise de variância (ANOVA) e testes paramétricos. É muito importante destacar, que independentemente de sua área de atuação, seja educação, engenharia, saúde ou negócios dominar esse conceito é ajuda para interpretar dados com rigor científico.
Como calcular o z-score para valores individuais de observações únicas
O z-score para um valor individual é obtido pela fórmula:
\[ Z = \frac{X – \mu}{\sigma} \]
Inclusive, onde \( X \) é o valor observado, \( \mu \) é a média populacional e \( \sigma \) é o desvio padrão populacional. Por exemplo, se a altura média de adultos em um país é 170 cm com desvio padrão de 10 cm, e uma pessoa mede 185 cm, seu z-score será:
\[ Z = \frac{185 – 170}{10} = 1{,}5 \]
Já que isso indica que a altura dessa pessoa está 1,5 desvios padrão acima da média nacional. Visto que ao calcular z-scores individuais, você pode identificar rapidamente se um dado é comum ou extremo dentro de sua distribuição de origem.
Como utilizar o z-score para médias amostrais de distribuição
Só para ilustrar, quando trabalhamos com a média de uma amostra e não com um valor individual, usamos o erro padrão da média no denominador. A fórmula do correta do score padrão Z para amostras é:
\[ Z = \frac{\bar{X} – \mu}{\sigma / \sqrt{n}} \]
Onde \( \bar{X} \) é a média amostral, \( \mu \) é a média populacional, \( \sigma \) é o desvio padrão populacional e \( n \) é o tamanho da amostra. Suponha que a média de uma amostra de 36 estudantes seja 78 em um teste cuja média populacional é 75 e desvio padrão é 12. O Z-score será:
\[ Z = \frac{78 – 75}{12 / \sqrt{36}} = \frac{3}{2} = 1{,}5 \]
Ou seja, esse resultado permite avaliar se a média da amostra é significativamente diferente da média populacional, um passo essencial em testes de hipóteses.
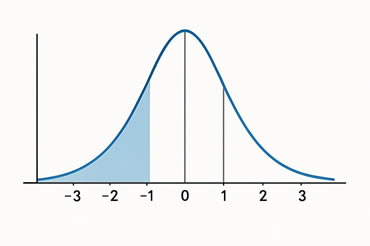
Área sob a curva da estatística z para probabilidade acumulada
Uma vez calculado o z-score, é possível encontrar a probabilidade associada usando a tabela da distribuição normal padrão ou uma calculadora estatística. Desse modo, essa probabilidade representa a área sob a curva à esquerda do score padrão z. Por exemplo, um Z = 1,5 corresponde aproximadamente a 0,9332, ou seja, há 93,32% de chance de obter um valor menor ou igual ao observado.
De forma resumida, se você deseja a probabilidade de um valor ser maior que X, basta fazer \( 1 – P(Z) \). Para intervalos entre dois valores, subtraia as probabilidades acumuladas. Assim, o z score serve como uma ponte entre dados brutos e interpretação probabilística.
O valor do percentil inverso (z crítico) da probabilidade para o valor z
Certamente, você conhece a probabilidade desejada e quer descobrir o valor correspondente na escala original. Então, nesse caso, inverte-se a fórmula do Z-score:
\[ X = \mu + Z \cdot \sigma \]
Por exemplo, se você quer saber qual nota separa os 10% melhores alunos em uma prova com média 70 e desvio padrão 8, primeiro encontra o Z correspondente ao percentil 90 (Z = 1,28). Depois:
\[ X = 70 + 1{,}28 \cdot 8 = 80{,}24 \]
Portanto, notas acima de 80,24 estão no top 10%. Para entender melhor, esse cálculo inverso é amplamente usado em seleção de candidatos, definição de limites clínicos e benchmarks de desempenho.
Os intervalos de confiança estimação por intervalo da média populacional
Em primeiro lugar, os intervalos de confiança estimam a faixa em que a verdadeira média populacional provavelmente se encontra, com base em uma amostra. Quando o desvio padrão populacional é conhecido, usa-se o z-score crítico por exemplo: 1,96 para 95% de confiança:
\[ \text{IC} = \bar{X} \pm Z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}} \]
Observe esse cenário e suponha uma amostra de 100 pessoas com média de renda R$ 3.000,00 desvio padrão populacional de R$ 500 e confiança de 95%. Portanto, o intervalo será:
\[ 3000 \pm 1{,}96 \cdot \frac{500}{\sqrt{100}} = 3000 \pm 98 \]
Ou seja, temos 95% de confiança de que a renda média real está entre R$ 2.902 e R$ 3.098. Sendo assim, esse método é vital em pesquisas de mercado, estudos epidemiológicos e auditorias.
Teste de hipóteses z teste de significância para a média
Atualmente o teste Z é usado para verificar se uma hipótese sobre a média populacional é plausível. As etapas são:
- Formular H₀ e H₁;
- Calcular o Z-score da amostra;
- Comparar com o valor crítico ou usar o p-valor.
Por exemplo, se um fabricante afirma que seus pacotes têm 500g em média, e uma amostra de 64 pacotes tem média 495g com σ = 20g, o Z será:
\[ Z = \frac{495 – 500}{20 / \sqrt{64}} = \frac{-5}{2{,}5} = -2 \]
Com α = 0,05 (bilateral), o valor crítico é ±1,96. Como -2 < -1,96, rejeita-se H₀: há evidência de que os pacotes pesam menos que o declarado. O teste Z é muito robusto, simples e amplamente aplicável quando as condições de normalidade e conhecimento de σ são satisfeitas.
Como dominar o score padrão com ou sem calculadora se z-score
Para se tornar expert no uso do z-score, pratique com conjuntos de dados como notas escolares, medidas biométricas, tempos de resposta, etc. Ocasionalmente, comece interpretando z-scores individuais, depois avance para intervalos de confiança e testes de hipóteses. Em seguida, utilize gráficos da curva normal para visualizar áreas de probabilidade e vefiricar sua intuição estatística.
Por fim, use ferramentas digitais como a nossa calculadora de z-score mostra cada passo do cálculo, desde a padronização até a probabilidade final, tornando o aprendizado mais fácil. Além disso, resolva exercícios diversos com dados unilaterais, bilaterais, amostrais e populacionais para facilitar o aprendizado. Concluindo, quanto mais você aplicar o z-score em situações reais, mais natural se tornará sua interpretação e uso em análises estatísticas.
FAQ – Perguntas Frequentes sobre Z-score
O z-score negativo indica que o valor está abaixo da média da distribuição. Já que quanto mais negativo, mais distante da média.
O z-score pode ser calculado para qualquer distribuição, mas sua interpretação probabilística via tabela normal só é válida se os dados forem aproximadamente normais ou a amostra for grande Teorema Central do Limite.
O z-score usa o desvio padrão populacional σ e é usado quando σ é conhecido. O T-score usa o desvio padrão amostral s e é usado quando σ é desconhecido, especialmente com amostras pequenas.
É o valor de Z que delimita a região de rejeição em um teste de hipóteses. Por exemplo, para α = 0,05 bilateral, o Z crítico é ±1,96.
Use uma tabela Z, uma calculadora estatística ou software (como Microsoft Excel com =NORM.S.DIST(z;VERDADEIRO)). A tabela fornece a área acumulada à esquerda do Z.
Sim! Valores com |Z| > 2 ou |Z| > 3 são frequentemente considerados outliers, pois estão muito distantes da média em termos de desvios padrão.
Insira a média, o desvio padrão e o valor observado ou a média amostral e tamanho da amostra. Escolha o tipo de cálculo: Z individual, probabilidade, valor inverso, intervalo de confiança ou teste de hipóteses. Clique em calcular e veja o resultado com explicação detalhada.